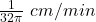If a snowball melts so that its surface area decreases at a rate of 3 cm2/min, how do you find the rate at which the diameter decreases when

Question

If a snowball melts so that its surface area decreases at a rate of 3 cm2/min, how do you find the rate at which the diameter decreases when the diameter is 12 cm?

in progress 0
Nho 4 years 2021-08-20T09:17:59+00:00 1 Answers 20 views 0

Answers ( )

  1. Maris
    0
    2021-08-20T09:19:21+00:00
    Reply

    Answer:

    \frac{1}{32\pi} \ cm/min

    Explanation:

    -Assume the snowball is a spherically perfect:

    A=4\pi r^2#

    A=4\pi(\frac{D}{2})^2\\\\A=\pi D^2

    Therefore, at the time of interest, we plug the value of dA/dt and r(r=6cm):

    D=2r\\\\\frac{dA}{dt}=4\pi(2r)\frac{dr}{dt}=8\pi r \frac{dr}{dt}\\\\-1.5=8\pi(6)\frac{dr}{dt}=48\pi \frac{dr}{dt}\\\\\frac{dr}{dt}=-\frac{1}{32\pi}

    Hence, the diameter is decreasing at a rate of  \frac{1}{32\pi} \ cm/min

Leave an answer

Browse

Giải phương trình 1 ẩn: x + 2 - 2(x + 1) = -x . Hỏi x = ? ( )