Find the domain of the function y = 3 tan(23x)

Question

Find the domain of the function y = 3 tan(23x)

in progress 0
Euphemia 3 years 2021-07-17T23:25:57+00:00 1 Answers 1 views 0

Answers ( )

  1. Orla
    0
    2021-07-17T23:27:41+00:00
    Reply

    Answer:

    \mathbb{R} \backslash \displaystyle \left\lbrace \left. \frac{1}{23}\, \left(k\, \pi + \frac{\pi}{2}\right) \; \right| k \in \mathbb{Z} \right\rbrace.

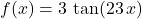    In other words, the x in f(x) = 3\, \tan(23\, x) could be any real number as long as 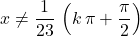x \ne \displaystyle \frac{1}{23}\, \left(k\, \pi + \frac{\pi}{2}\right) for all integer k (including negative integers.)

    Step-by-step explanation:

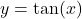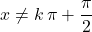    The tangent function y = \tan(x) has a real value for real inputs x as long as the input x \ne \displaystyle k\, \pi + \frac{\pi}{2} for all integer k.

    Hence, the domain of the original tangent function is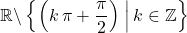 \mathbb{R} \backslash \displaystyle \left\lbrace \left. \left(k\, \pi + \frac{\pi}{2}\right) \; \right| k \in \mathbb{Z} \right\rbrace.

    On the other hand, in the function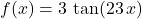 f(x) = 3\, \tan(23\, x), the input to the tangent function is replaced with (23\, x).

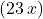    The transformed tangent function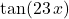 \tan(23\, x) would have a real value as long as its input 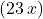(23\, x) ensures that 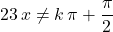23\, x\ne \displaystyle k\, \pi + \frac{\pi}{2} for all integer k.

    In other words,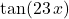 \tan(23\, x) would have a real value as long as x\ne \displaystyle \frac{1}{23} \, \left(k\, \pi + \frac{\pi}{2}\right).

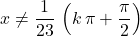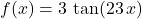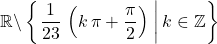    Accordingly, the domain of f(x) = 3\, \tan(23\, x) would be \mathbb{R} \backslash \displaystyle \left\lbrace \left. \frac{1}{23}\, \left(k\, \pi + \frac{\pi}{2}\right) \; \right| k \in \mathbb{Z} \right\rbrace.

Leave an answer

Browse

Giải phương trình 1 ẩn: x + 2 - 2(x + 1) = -x . Hỏi x = ? ( )