Share
Find the dimensions of a rectangle with area 3 square meters whose perimeter is as small as possible.
Question
Find the dimensions of a rectangle with area 3 square meters whose perimeter is as small as possible.
in progress
0
Mathematics
4 years
2021-08-05T18:27:04+00:00
2021-08-05T18:27:04+00:00 1 Answers
13 views
0

Answers ( )
Answer:
The perimeter is minimum for Length and width both are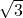 .
.
Step-by-step explanation:
Area, A = 3 square metre
Let the length is L and width is W.
Area = L W
3 = L W…..(1)
The perimeter is given by
P = 2 (L + W)
Substitute the value of from (1)
Now
It is alays positive, so the perimeter is minimum.