Find an equation for the perpendicular bisector of the line segment whose endpoints are (-4,-5)and (8,-9)

Question

Find an equation for the perpendicular bisector of the line segment whose endpoints are (-4,-5)and (8,-9)

in progress 0
Thành Đạt 4 years 2021-08-14T16:06:22+00:00 1 Answers 16 views 0

Answers ( )

  1. ngochoa
    0
    2021-08-14T16:07:46+00:00
    Reply

    Answer:

    y = 3x – 13

    Step-by-step explanation:

    slope of line segment is -1/3 so a segment perpendicular to this would need a slope of 3

    the midpoint for the segment is (2, -7); midpoint formula is [(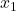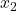x_{1}+x_{2}/2), (y_{1}+y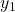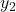_{2}/2)]

    using slope of 3 and point (2, -7) we can plug into y = mx + b

    -7 = 3(2) + b

    -7 = 6 + b

    b = -13

Leave an answer

Browse

Giải phương trình 1 ẩn: x + 2 - 2(x + 1) = -x . Hỏi x = ? ( )