Find all points on the x-axis that are 14 units from the point (4, -7). (Simplify your answer. Type an ordered pair. Use a comma

Question

Find all points on the x-axis that are 14 units from the point (4, -7).

(Simplify your answer. Type an ordered pair. Use a comma to separate answers as needed.)

in progress 0
Ngọc Diệp 4 years 2021-09-01T01:06:09+00:00 1 Answers 24 views 0

Answers ( )

  1. Delwyn
    0
    2021-09-01T01:07:45+00:00
    Reply

    Answer:

    The points are: (16.12,0),(-8.12,0).

    Step-by-step explanation:

    Solving a quadratic equation:

    Given a second order polynomial expressed by the following equation:

    ax^{2} + bx + c, a\neq0.

    This polynomial has roots x_{1}, x_{2} such that ax^{2} + bx + c = a(x - x_{1})*(x - x_{2}), given by the following formulas:

    x_{1} = \frac{-b + \sqrt{\bigtriangleup}}{2*a}

    x_{2} = \frac{-b - \sqrt{\bigtriangleup}}{2*a}

    \bigtriangleup = b^{2} - 4ac

    Distance between two points:

    Suppose we have two points, (x_1,y_1) and (x_2,y_2). The distance between them is given by:

    D = \sqrt{(x_2-x_1)^2+(y_2-y_1)^2}

    Find all points on the x-axis that are 14 units from the point (4, -7).

    Being on the x-axis mean that they have y-coordinate equal to 0, so the point is (x,0).

    The distance is 14. So

    \sqrt{(x-4)^2+(0-(-7))^2} = 14

    \sqrt{x^2 - 8x + 16 + 49} = 14

    \sqrt{x^2 - 8x + 65} = 14

    (\sqrt{x^2 - 8x + 65})^2 = 14^2

    x^2 - 8x + 65 - 196 = 0

    x^2 - 8x - 131 = 0

    So a = 1, b = -8, c = -131

    \bigtriangleup = (-8)^{2} - 4(1)(-131) = 588

    x_{1} = \frac{-(-8) + \sqrt{588}}{2} = 16.12

    x_{1} = \frac{-(-8) - \sqrt{588}}{2} = -8.12

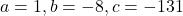
    The points are: (16.12,0),(-8.12,0).

Leave an answer

Browse

Giải phương trình 1 ẩn: x + 2 - 2(x + 1) = -x . Hỏi x = ? ( )