F(x) = x/x+6, [1, 12] If it satisfies the hypotheses, find all numbers c that satisfies the conclusion of the Mean Value Theorem. (Enter you

Question

F(x) = x/x+6, [1, 12] If it satisfies the hypotheses, find all numbers c that satisfies the conclusion of the Mean Value Theorem. (Enter your answers as a comma-separated list. If it does not satisfy the hypotheses, enter DNE).

in progress 0
Eirian 4 years 2021-08-27T10:20:41+00:00 1 Answers 5 views 0

Answers ( )

  1. mocmien2
    0
    2021-08-27T10:22:09+00:00
    Reply

    Answer:

    The answer is “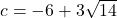{c=-6+3\sqrt{14}“

    Step-by-step explanation:

    Given:

    \to F(x) = \frac{x}{x+6} , \ [1, 12]

    \to f'(c)=\frac{f(b)-f(a)}{b-a}

    As per the given intervals:

    [1,12]\\\\ a=1 \\ b=12.

    Calculating the values of f(a) and f(b).

    \to f(1)=\frac{1}{1+6}= \frac{1}{7} \\\\ \to f(2)=\frac{12}{12+6}= \frac{12}{18}=\frac{2}{3} \\\\ \to f(x)=\frac{x}{x+6}\\\\

    \to f\:'\left(x\right)=\frac{d}{dx}\left(\frac{x}{x+6}\right)\: \\\\

             =\frac{\frac{d}{dx}\left(x\right)\left(x+6\right)-\frac{d}{dx}\left(x+6\right)x}{\left(x+6\right)^2} \\\\=\frac{1\cdot \left(x+6\right)-1\cdot \:x}{\left(x+6\right)^2}\\\\

    \to f'(x)=\frac{6}{\left(x+6\right)^2}

    Calculating the value of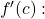 \ f'(c):

    \to \mathbf{f\:'\left(c\right)=\frac{6}{\left(c+6\right)^2}}

    Replacement of the values in the mean theorem of value now.

    \to \frac{6}{\left(c+6\right)^2}=\frac{\frac{2}{3}-\frac{1}{7}}{12-1}\\\\\to \frac{6}{\left(c+6\right)^2}=\frac{\frac{11}{21}}{11}\\\\\to \frac{6}{\left(c+6\right)^2}=\frac{1}{21}\\\\

     Apply the cross multiplication:

    \to (c+6)^2=126 \\\\\to c^2+12c +36= 126\\\\\to c^2+12c +36-126= 126-126 \\\\\to c^2+12c -90= 0\\\\\to c=\frac{-12\pm \sqrt{12^2-4\cdot \:1\left(-90\right)}}{2\cdot \:1}\\\\ \to \mathbf{c=-6+3\sqrt{14}} \\\\

Leave an answer

Browse

Giải phương trình 1 ẩn: x + 2 - 2(x + 1) = -x . Hỏi x = ? ( )