Share
Determine the wavelength of an electron that has a kinetic energy of 1.15 × 10^{-19} J. Report your answer in units of nm to the correct num
Question
Lost your password? Please enter your email address. You will receive a link and will create a new password via email.
Answers ( )
Answer:
The electron has a wavelength of 1448 nanometers.
Explanation:
The wavelength of the electron can be determined by means of the de Broglie wavelength.
Where h is the Planck’s constant and p is the momentum
The velocity can be found by means of the kinetic energy equation.
Therefore, equation 3 can be replaced in equation 2
Where m is the mass of the electron and KE its kinetic energy.
But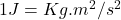
Finally, the wavelength can be expressed in terms of nanometers:
Hence, the electron has a wavelength of 1448 nanometers.