Consider the following quadratic equation. y = x2 – 8x + 4 Which of the following statements about the equation are true? The graph of the e

Question

Consider the following quadratic equation. y = x2 – 8x + 4 Which of the following statements about the equation are true? The graph of the equation has a minimum. When y = 0, the solutions of the equation are a = 4 + 2V3 o When y = 0, the solutions of the equation are r x = 8 + 2V2. o The extreme value of the graph is at (4,-12). The extreme value of the graph is at (8,-4). U The graph of the equation has a maximum. Submit​

in progress 0
Thạch Thảo 4 years 2021-09-05T12:40:59+00:00 1 Answers 16 views 0

Answers ( )

  1. danthu
    0
    2021-09-05T12:42:04+00:00
    Reply

    Answer:

    The graph of the equation has a minimum.

    When y = 0, the solutions are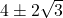 4 \pm 2\sqrt{3}

    The extreme value of the graph is (4,-12).

    Step-by-step explanation:

    Solving a quadratic equation:

    Given a second order polynomial expressed by the following equation:

    ax^{2} + bx + c, a\neq0.

    This polynomial has roots x_{1}, x_{2} such that ax^{2} + bx + c = a(x - x_{1})*(x - x_{2}), given by the following formulas:

    x_{1} = \frac{-b + \sqrt{\Delta}}{2*a}

    x_{2} = \frac{-b - \sqrt{\Delta}}{2*a}

    \Delta = b^{2} - 4ac

    Vertex of a quadratic function:

    Suppose we have a quadratic function in the following format:

    f(x) = ax^{2} + bx + c

    It’s vertex is the point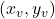 (x_{v}, y_{v})

    In which

    x_{v} = -\frac{b}{2a}

    y_{v} = -\frac{\Delta}{4a}

    Where

    \Delta = b^2-4ac

    If a<0, the vertex is a maximum point, that is, the maximum value happens at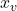 x_{v}, and it’s value is y_{v}.

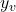    y = x2 – 8x + 4

    Quadratic equation with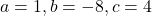 a = 1, b = -8, c = 4

    a is positive, so it’s graph has a minimum.

    Solutions when y = 0

    \Delta = b^2-4ac = 8^2 - 4(1)(4) = 64 - 16 = 48

    x_{1} = \frac{-(-8) + \sqrt{48}}{2} = \frac{8 + 4\sqrt{3}}{2} = 4 + 2\sqrt{3}

    x_{2} = \frac{-(8) - \sqrt{48}}{2} = \frac{8 - 4\sqrt{3}}{2} = 4 - 2\sqrt{3}

    When y = 0, the solutions are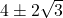 4 \pm 2\sqrt{3}

    Extreme value:

    The vertex. So

    x_{v} = -\frac{-8}{2} = 4

    y_{v} = -\frac{48}{4} = -12

    The extreme value of the graph is (4,-12).

Leave an answer

Browse

Giải phương trình 1 ẩn: x + 2 - 2(x + 1) = -x . Hỏi x = ? ( )