Consider the following function. x6 1 + x2 dx (a) Determine an appropriate trigonometric substitution. Use x = sin(θ), where − π 2 ≤ θ ≤ π 2

Question

Consider the following function. x6 1 + x2 dx (a) Determine an appropriate trigonometric substitution. Use x = sin(θ), where − π 2 ≤ θ ≤ π 2 , since the integrand contains the expression 1 + x2 . Use x = tan(θ), where − π 2 < θ < π 2 , since the integrand contains the expression 1 + x2 . Use x = sec(θ), where 0 ≤ θ < π 2 or π ≤ θ < 3π 2 , since the integrand contains the expression 1 + x2 . (b) Apply the substitution to transform the integral into a trigonometric integral. Do not evaluate the integral. x6 1 + x2 dx = dθ

in progress 0
Yến Oanh 4 years 2021-08-21T21:17:20+00:00 1 Answers 6 views 0

Answers ( )

  1. ngochoa
    0
    2021-08-21T21:18:41+00:00
    Reply

    Answer:

    Step-by-step explanation:

    In the first part, we are given the function:

    \int \dfrac{x^6}{\sqrt{1+x}^2} \ dx

    Suppose we make x = tan θ

    Then dx = sec² θ.dθ

    = \int \dfrac{tan^6 (\theta)}{\sqrt{1+ tan ^2 \theta }}* dx

    = \int \dfrac{tan^6 (\theta)}{\sqrt{1+ tan ^2 \theta }}* sec ^2 (\theta) * d\theta

    Since; sec² θ – tan² θ = 1

    sec² θ = 1+ tan² θ

    sec \ \theta = \sqrt{1 + tan^2 \ \theta}

    ∴

    = \int \dfrac{tan^6 (\theta)}{sec \ \theta}* sec ^2 (\theta) * d\theta

    = \int tan^6 (\theta)* sec (\theta) * d\theta

    Thus; In the first part, Use x = tan θ, where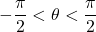  - \dfrac{\pi}{2} < \theta <\dfrac{\pi}{2}, since the integrand comprise the expression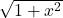 \sqrt{1+x^2}

    From the second part by using substitution method;

    \int \dfrac{x^6}{\sqrt{1+x^2}} \ dx = \int \mathbf{tan^6(\theta) * sec ( \theta) } \ d \theta

Leave an answer

Browse

Giải phương trình 1 ẩn: x + 2 - 2(x + 1) = -x . Hỏi x = ? ( )