Consider a steel tape measure with cross-sectional area, A = 0.0625 inches squared, and length L = 3, 600 inches at room temperature. How mu

Question

Consider a steel tape measure with cross-sectional area, A = 0.0625 inches squared, and length L = 3, 600 inches at room temperature. How much error will occur if this tape measure is used on a hot day? Assume it is 130F and the coefficient of thermal expansion is α = 5× 10 −6 1/F. Does the error depend on the distance being measured?

in progress 0
RI SƠ 4 years 2021-08-19T19:08:08+00:00 1 Answers 39 views 0

Answers ( )

  1. Bo
    0
    2021-08-19T19:09:38+00:00
    Reply

    Answer:

    e = -0.00031 ( the -ve sign is due to the increase in length)

    The error depends on the distance measured

    Explanation:

    Cross Sectional Area of the tape, A = 0.0625 in²

    Length of the steel tape, L = 3600 in

    Normal room temperature, T₁ = 68°F

    Temperature of the hot day, T₂ = 130°F

    ΔT = T₂  – T₁ = 130 – 68

    ΔT = 62°F

    Coefficient of Linear expansion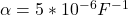 \alpha = 5 * 10^{-6} F^{-1}

    The coefficient of linear expansion is given by the formula:

    \alpha = \frac{\triangle L}{L* \triangle T} \\\triangle L = \alpha L \triangle T\\\triangle L = 5* 10^{-6} * 3.6* 10^3 * 62\\\triangle L = 1.11 6 in

    Since the length is increased, the error will be given by the formula:

    e = \frac{-\triangle L}{L} \\\\e = \frac{-1.116}{3600}

    e = -0.00031 ( the -ve sign is due to the increase in length)

    Since the error is a function of length and change in length, it depends on the distance measured

Leave an answer

Browse

Giải phương trình 1 ẩn: x + 2 - 2(x + 1) = -x . Hỏi x = ? ( )