. Compute the required sample size given the required confidence in the sample results is 99.74% (Z score of 3). The level of allowable samp

Question

. Compute the required sample size given the required confidence in the sample results is 99.74% (Z score of 3). The level of allowable sampling error is 5% and the estimated population standard deviation is unknown. Q/A6.1. Compute the required sample size given the required confidence in the sample results is 99.74% (Z score of 3). The level of allowable sampling error is 5% and the estimated population standard deviation is unknown.

in progress 0
Adela 4 years 2021-08-21T21:09:46+00:00 1 Answers 31 views 0

Answers ( )

  1. bonexptip
    0
    2021-08-21T21:11:42+00:00
    Reply

    Answer:

    900 sample size

    Step-by-step explanation:

    To determine the sample size for a proportion, the margin of error formula is used to determine this:

    E=Z_{\frac{\alpha}{2} }*\sqrt{\frac{\hat p \hat q}{{n} }

    n=\hat p \hat q*(\frac{Z_{\frac{\alpha}{2} }}{E} )^2

    Where p is the proportion, E is the margin of error, n is the sample size, q = 1 – p,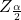 Z_\frac{\alpha }{2} is the z score.

    Since the proportion is not known, the sample size needed to guarantee the confidence interval and error is at p = 0.5 and q = 1 – p = 1 – 0.5 = 0.5

    E = 5% = 0.05,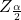 Z_\frac{\alpha }{2} = 3. Hence:

    n=0.5*0.5*(\frac{3}{0.05} )^2\\\\n = 900

Leave an answer

Browse

Giải phương trình 1 ẩn: x + 2 - 2(x + 1) = -x . Hỏi x = ? ( )