Cannonball a is launched across level ground with speed v₀ at an angle of 45. Cannonball b is launched from the same location with the same

Question

Cannonball a is launched across level ground with speed v₀ at an angle of 45. Cannonball b is launched from the same location with the same speed v₀ at an angle 60. Which cannonball spends more time in the air?

in progress 0
Sigridomena 3 years 2021-09-05T16:49:59+00:00 1 Answers 7 views 0

Answers ( )

  1. RobertKer
    0
    2021-09-05T16:51:43+00:00
    Reply

    Answer:

    Cannonball b spends more time in the air than cannonball a.

    Explanation:

    Starting with the definition of acceleration, we have that:

    a=\frac{\Delta v}{\Delta t}\\\\\Delta t= \frac{\Delta v}{a}

    Since both cannonballs will stop in their maximum height, their final velocity is zero. And since the acceleration in the y-axis is g, we have:

    \Delta t= -\frac{v_{oy}}{g}

    Now, this time interval is from the moment the cannonballs are launched to the moment of their maximum height, exactly the half of their time in the air. So their flying time t_f is (the minus sign is ignored since we are interested in the magnitudes only):

    t_f=2\frac{v_{oy}}{g}

    Then, we can see that the time the cannonballs spend in the air is proportional to the vertical component of the initial velocity. And we know that:

    v_{oy}=v_o\sin\theta\\\\\implies t_f=2\frac{v_o\sin\theta}{g}

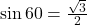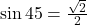    Finally, since \sin60\°=\frac{\sqrt{3} }{2} and \sin45\°=\frac{\sqrt{2} }{2}, we can conclude that:

    t_{fa}=\sqrt{2}\frac{v_o }{g} \\\\t_{fb}=\sqrt{3}\frac{v_o }{g}\\\\\implies t_{fb}>t_{fa}

    In words, the cannonball b spends more time in the air than cannonball a.

Leave an answer

Browse

Giải phương trình 1 ẩn: x + 2 - 2(x + 1) = -x . Hỏi x = ? ( )