Calculate the current in a 75 Ω resistor when a potential difference of 115 V is placed across it. What will the current be if the resistor is replaced with a 47 Ω resistor?
Question
Question
Calculate the current in a 75 Ω resistor when a potential difference of 115 V is placed across it. What will the current be if the resistor is replaced with a 47 Ω resistor?
Answer:
[tex]i = 1.533\,A[/tex], [tex]i = 2.447\,A[/tex]
Explanation:
The current is determined by the Ohm’s Law:
[tex]\Delta V = i \cdot R[/tex]
[tex]i = \frac{\Delta V}{R}[/tex]
The current in a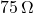 [tex]75\,\Omega[/tex] Resistor is:
[tex]i=\frac{115\,V}{75\,\Omega}[/tex]
[tex]i = 1.533\,A[/tex]
If current resistor is replaced by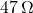 [tex]47\,\Omega[/tex] model, then the current is:
[tex]i = \frac{115\,V}{47\,\Omega}[/tex]
[tex]i = 2.447\,A[/tex]
Answer:
1.53A; 2.45A
Explanation:
According to ohm’s law which states that the current passing through a metallic conductor at constant temperature is directly proportional to the potential difference across its ends. Mathematically,
V = IR where;
V is the potential difference
I is the current
R is the Resistance.
If a a potential difference of 115 V is placed across 75ohms resistor, the current in the resistor can be calculated as;
I = V/R where;
V = 115V
R = 75ohms
I = 115/75
I = 1.53A
If the resistor is replaced with a 47ohms resistor, the current I’m the resistor will be calculated as;
I = V/R
I = 115/47
I = 2.45A
According to the answers, the current decreases with increasing resistance because resistance tends to oppose the flow of current.