Bob ‘s daily commute time is randomly distributed with a minimum of 20 minutes, a maximum of 61 minutes, and the most common length is 30 mi

Question

Bob ‘s daily commute time is randomly distributed with a minimum of 20 minutes, a maximum of 61 minutes, and the most common length is 30 minutes. What is the probability that his commute today took more than 35 minutes?

in progress 0
Thiên Ân 4 years 2021-07-20T19:31:15+00:00 1 Answers 40 views 0

Answers ( )

  1. ngochoa
    0
    2021-07-20T19:33:05+00:00
    Reply

    Answer:

    0.6341 = 63.41% probability that his commute today took more than 35 minutes

    Step-by-step explanation:

    Randomly distributed = Uniform distribution.

    A distribution is called uniform if each outcome has the same probability of happening.

    The uniform distributon has two bounds, a and b, and the probability of finding a value higher than x is given by:

    P(X > x) = \frac{b - x}{b - a}

    Randomly distributed with a minimum of 20 minutes, a maximum of 61 minutes.

    This means that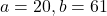 a = 20, b = 61.

    What is the probability that his commute today took more than 35 minutes?

    P(X > 35) = \frac{61 - 35}{61 - 20} = 0.6341

    0.6341 = 63.41% probability that his commute today took more than 35 minutes

Leave an answer

Browse

Giải phương trình 1 ẩn: x + 2 - 2(x + 1) = -x . Hỏi x = ? ( )