An object suspended from a spring vibrates with simple harmonic motion. Part A At an instant when the displacement of the object is equal to

Question

An object suspended from a spring vibrates with simple harmonic motion. Part A At an instant when the displacement of the object is equal to one-fourth the amplitude, what fraction of the total energy of the system is kinetic

in progress 0
Neala 4 years 2021-08-26T19:23:02+00:00 1 Answers 8 views 0

Answers ( )

  1. Eirian
    0
    2021-08-26T19:24:12+00:00
    Reply

    Complete Question

    An object suspended from a spring vibrates with simple harmonic motion.

    a. At an instant when the displacement of the object is equal to one-half the amplitude, what fraction of the total energy of the system is kinetic?

    b. At an instant when the displacement of the object is equal to one-half the amplitude, what fraction of the total energy of the system is potential?

    Answer:

    a

    The fraction of the total energy of the system is kinetic energy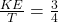  \frac{KE}{T} = \frac{3}{4}

    b

    The fraction of the total energy of the system is potential energy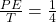  \frac{PE}{T} = \frac{1}{4}

    Explanation:

    From the question we are told that

        The displacement of the system is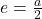  e = \frac{a}{2}

    where a is the amplitude

         

    Let denote the potential energy as PE  which is mathematically represented as

               PE = \frac{1}{2} * k* x^2

    =>       PE = \frac{1}{2} * k* [\frac{a}{2} ]^2

              PE = k* [\frac{a^2}{8} ]

     Let denote the total energy as T which is mathematically represented as

               T = \frac{1}{2} * k * a^2

    Let denote the kinetic energy as  KE  which is mathematically represented as

          KE = T -PE

      =>     KE =k [ \frac{a^2}{2} - \frac{a^2}{8} ]

    =>      KE =k [ \frac{3}{8} a^2 ]

    Now the fraction of the total energy that is kinetic energy is  

           \frac{KE}{T} = \frac{ \frac{3ka^2}{8} }{\frac{ka^2}{2} }

           \frac{KE}{T} = \frac{3}{4}

    Now the fraction of the total energy that is potential energy is  

          \frac{PE}{T} = \frac{\frac{k a^2}{8} }{\frac{k a^2}{2} }

          \frac{PE}{T} = \frac{1}{4}

Leave an answer

Browse

Giải phương trình 1 ẩn: x + 2 - 2(x + 1) = -x . Hỏi x = ? ( )