Share
An object has a position given by the radius vector r = [2.0 m + (3.00 m/s)t](i)+ [3.0 m – (2.00 m/s^2)t^2](j). Here (i) and (j) are the uni
Question
An object has a position given by the radius vector r = [2.0 m + (3.00 m/s)t](i)+ [3.0 m – (2.00 m/s^2)t^2](j). Here (i) and (j) are the unit vectors along x and y and all quantities are in SI units. What is the speed and magnitude of the acceleration in m/s^2 of the object at time t = 2.00 s
in progress
0
Physics
4 years
2021-08-20T22:18:17+00:00
2021-08-20T22:18:17+00:00 1 Answers
141 views
0

Answers ( )
Answer:
The speed of the object is (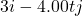 )m/s
)m/s
The magnitude of the acceleration is 4.00m/s²
Explanation:
Given – position vector;
r = (2.0 + 3.00t)i + (3.0 – 2.00t²)j ——————-(i)
To get the speed vector ( ), take the first derivative of equation (i) with respect to time t as follows;
), take the first derivative of equation (i) with respect to time t as follows;
To get the acceleration vector ( ), take the first derivative of the speed vector in equation(ii) as follows;
), take the first derivative of the speed vector in equation(ii) as follows;
The magnitude of the acceleration |a| is therefore given by
|a| = |-4.00|
|a| = 4.00 m/s²
In conclusion;
the speed of the object is (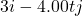 )m/s
)m/s
the magnitude of the acceleration is 4.00m/s²