Share
An Atwood machine consists of two masses hanging from the ends of a rope that passes over a pulley. Assume that the rope and pulley are mass
Question
An Atwood machine consists of two masses hanging from the ends of a rope that passes over a pulley. Assume that the rope and pulley are massless and that there is no friction in the pulley. If the masses have the values m 1 = 17.7 kg m1=17.7 kg and m 2 = 11.1 kg, m2=11.1 kg, find the magnitude of their acceleration a a and the tension T T in the rope. Use g = 9.81 m/s 2 .
in progress
0
Physics
4 years
2021-08-21T21:30:00+00:00
2021-08-21T21:30:00+00:00 2 Answers
21 views
0

Answers ( )
Answer:
Explanation:
m1 = 17.7 kg
m2 = 11.1 kg
Let a be the acceleration and T be the tension in the string.
use Newton’s second law
m1 g – T = m1 x a ….(1)
T – m2 g = m2 x a ….. (2)
Adding both the equations
(m1 – m2) g = ( m1 + m2 ) x a
(17.7 – 11.1 ) x 9.8 = (17.7 + 11.1) x a
64.68 = 28.8 a
a = 2.25 m/s²
Put the value of a in equation (1)
17.7 x 9.8 – T = 17.7 x 2.25
173.46 – T = 39.825
T = 133.64 N
Explanation:
According to Newton’s second law of motion,
and,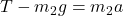 ……… (2)
……… (2)
When we add both equations, (1) and (2) then the expression obtained for “a” is as follows.
a =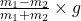
=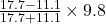
=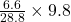
= 2.24
Now, putting the value of “a” in equation (1) then we will calculate the tension as follows.
173.46 – T = 39.648
T = 133.812 N
Thus, we can conclude that the magnitude of their acceleration is 2.24 and the tension T is 133.812 N in the rope.
and the tension T is 133.812 N in the rope.