Share
A wooden log 10 meters long is leaning against a vertical wall with its other end on the ground. The top end of the log is sliding down the
Question
A wooden log 10 meters long is leaning against a vertical wall with its other end on the ground. The top end of the log is sliding down the wall. When the top end is 6 meters from the ground, it slides down at 2m/sec. How fast is the bottom moving away from the wall at this instant?
in progress
0
Mathematics
3 years
2021-07-31T05:32:39+00:00
2021-07-31T05:32:39+00:00 1 Answers
8 views
0

Answers ( )
Answer:
Step-by-step explanation:
This is a related rates problem from calculus using implicit differentiation. The main equation is Pythagorean’s Theorem. Basically, what we are looking for is when y = 6 and
when y = 6 and 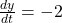 .
.
The equation for Pythagorean’s Theorem is
Since we are looking for , that can be our only unknown and everything else has to have a value. So what do we know?
, that can be our only unknown and everything else has to have a value. So what do we know?
If we construct a right triangle with 10 as the hypotenuse and use 6 for y, we can solve for x (which is the only unknown we have, actually). Using Pythagorean’s Theorem to solve for x:
x = 8.
NOW we can fill in the derivative and solve for .
.
Remember the derivative is