A tube is open only at one end. A certain harmonic produced by the tube has a frequency of 571 Hz. The next higher harmonic has a frequency

Question

A tube is open only at one end. A certain harmonic produced by the tube has a frequency of 571 Hz. The next higher harmonic has a frequency of 799 Hz. The speed of sound in air is 343 m/s. (a) What is the integer n that describes the harmonic whose frequency is 571 Hz? (b) What is the length of the tube?

B. A person hums into the top of a well (tube open at only one end) and finds that standing waves are established at frequencies of 36.1, 60.2, and 84.2 Hz. The frequency of 36.1 Hz is not necessarily the fundamental frequency. The speed of sound is 343 m/s. How deep is the well?

in progress 0
Sigridomena 3 years 2021-08-26T10:50:49+00:00 1 Answers 34 views 0

Answers ( )

  1. huyenthanh
    0
    2021-08-26T10:52:08+00:00
    Reply

    Answer:

    The answers to the question are

    (a) The integer n that describes the harmonic whose frequency is 571 Hz is 5

    (b) The length of the tube is 0.75 m.

    B. The depth of the well is 7.12 m.

    Explanation:

    The nth harmonic of a tube with one end closed is given by

    f_n = n(\frac{v}{4L}) and the next harmonic is

    f_{n+2} =(n+2)(\frac{v}{4L} )

    Therefore ividing the first two equations by each other we have

    \frac{f_{n+2}}{f_n} = \frac{n+2}{n} from which n = \frac{2}{\frac{f_{n+2}}{f_n} -1}

    Therefore the interger that descries the first harmonic is

    n =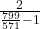 \frac{2}{\frac{799}{571} -1} = 5

    (b) We have the length of the pipe given by

    L = 5λ/4 but λ = v/f = 343/571 = 0.6 ∴ L  = 5*0.6/4 = 0.75 m

    B. From n =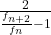 \frac{2}{\frac{f_{n+2}}{f_n} -1} we have

    n for the 36.1 Hz frequency

    n =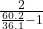 \frac{2}{\frac{60.2}{36.1} -1} = 3 Therefore λ = v/f = 343/36.1 = 9.5 m

    L = 3*λ/4 = 3*9.5/4 = 7.12 m

    The well is  7.12 m deep

Leave an answer

Browse

Giải phương trình 1 ẩn: x + 2 - 2(x + 1) = -x . Hỏi x = ? ( )