A torque of 36.5 N · m is applied to an initially motionless wheel which rotates around a fixed axis. This torque is the result of a directe

Question

A torque of 36.5 N · m is applied to an initially motionless wheel which rotates around a fixed axis. This torque is the result of a directed force combined with a friction force. As a result of the applied torque the angular speed of the wheel increases from 0 to 10.3 rad/s. After 6.10 s the directed force is removed, and the wheel comes to rest 60.6 s later.
(a) What is the wheel’s moment of inertia (in kg m2)? kg m
(b) What is the magnitude of the torque caused by friction (in N m)? N m
(c) From the time the directed force is initially applied, how many revolutions does the wheel go through?
______ revolutions

in progress 0
Gerda 4 years 2021-09-01T00:51:26+00:00 1 Answers 36 views 0

Answers ( )

  1. Maris
    0
    2021-09-01T00:52:44+00:00
    Reply

    Answer:

    21.6\ \text{kg m}^2

    3.672\ \text{Nm}

    54.66\ \text{revolutions}

    Explanation:

    \tau = Torque = 36.5 Nm

    \omega_i = Initial angular velocity = 0

    \omega_f = Final angular velocity = 10.3 rad/s

    t = Time = 6.1 s

    I = Moment of inertia

    From the kinematic equations of linear motion we have

    \omega_f=\omega_i+\alpha_1 t\\\Rightarrow \alpha_1=\dfrac{\omega_f-\omega_i}{t}\\\Rightarrow \alpha_1=\dfrac{10.3-0}{6.1}\\\Rightarrow \alpha_1=1.69\ \text{rad/s}^2

    Torque is given by

    \tau=I\alpha_1\\\Rightarrow I=\dfrac{\tau}{\alpha_1}\\\Rightarrow I=\dfrac{36.5}{1.69}\\\Rightarrow I=21.6\ \text{kg m}^2

    The wheel’s moment of inertia is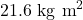 21.6\ \text{kg m}^2

    t = 60.6 s

    \omega_i = 10.3 rad/s

    \omega_f = 0

    \alpha_2=\dfrac{0-10.3}{60.6}\\\Rightarrow \alpha_1=-0.17\ \text{rad/s}^2

    Frictional torque is given by

    \tau_f=I\alpha_2\\\Rightarrow \tau_f=21.6\times -0.17\\\Rightarrow \tau=-3.672\ \text{Nm}

    The magnitude of the torque caused by friction is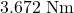 3.672\ \text{Nm}

    Speeding up

    \theta_1=0\times t+\dfrac{1}{2}\times 1.69\times 6.1^2\\\Rightarrow \theta_1=31.44\ \text{rad}

    Slowing down

    \theta_2=10.3\times 60.6+\dfrac{1}{2}\times (-0.17)\times 60.6^2\\\Rightarrow \theta_2=312.03\ \text{rad}

    Total number of revolutions

    \theta=\theta_1+\theta_2\\\Rightarrow \theta=31.44+312.03=343.47\ \text{rad}

    \dfrac{343.47}{2\pi}=54.66\ \text{revolutions}

    The total number of revolutions the wheel goes through is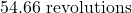 54.66\ \text{revolutions}.

Leave an answer

Browse

Giải phương trình 1 ẩn: x + 2 - 2(x + 1) = -x . Hỏi x = ? ( )