A thin uniform cylindrical turntable of radius 2.2 m and mass 35 kg rotates in a horizontal plane with an initial angular speed of 11 rad/s.

Question

A thin uniform cylindrical turntable of radius 2.2 m and mass 35 kg rotates in a horizontal plane with an initial angular speed of 11 rad/s. The turntable bearing is frictionless. A clump of clay of mass 17 kg is dropped onto the turntable and sticks at a point 1.5 m from the point of rotation.

Find the angular speed of the clay and turntable.

in progress 0
Khánh Gia 4 years 2021-08-15T22:50:58+00:00 2 Answers 29 views 0

Answers ( )

  1. Sigrid
    0
    2021-08-15T22:52:26+00:00
    Reply

    Answer:

    Explanation:

    Mass of turn table, M = 35 kg

    Radius of turn table, R = 2.2 m

    initial angular velocity, ω = 11 rad/s

    mass of clay, m = 17 kg

    distance of clay from centre of table, r = 1.5 m

    Let the final angular velocity is ω’.

    By the use of conservation of angular momentum

    I x ω = I’ x ω’

    where, I is the moment of inertia of the turn table = 0.5 MR²

    I = 0.5 x 35 x 2.2 x 2.2 = 84.7 kg m²

    I’ is the moment of inertia of the table and the clay lump.

    I’ = I + mr² = 84.7 + 17 x 1.5 x 1.5 = 122.95 kg m²

    Now

    84.7 x 11 = 122.95 x ω’

    ω’ = 7.78 rad/s  

  2. Latifah
    0
    2021-08-15T22:52:28+00:00
    Reply

    Explanation:

    The given data is as follows.

        M = 35 kg,    radius (r) = 2.2 m,

         m = 17 kg,     = 11 rad/s

    We assume that will be the final angular speed.

    Now, according to the conservation of angular momentum.

             L_{1} = L_{2}

    or,    I_{1} \times \omega_{1} = I_{2} \times \omega_{2}

    Putting the given values into the above formula as follows.

      I_{1} \times \omega_{1} = I_{2} \times \omega_{2}

       

    or,  

          = \frac{(0.5 \times 35 \times (2.2)^{2}) \times 11}{(0.5 \times 35 \times (2.2)^{2} + 17 \times (1.5)^{2})}

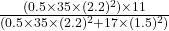
          = 7.58 rad/s

    Thus, we can conclude that the angular speed of the clay and turntable is 7.58 rad/s.

Leave an answer

Browse

Giải phương trình 1 ẩn: x + 2 - 2(x + 1) = -x . Hỏi x = ? ( )