A thin block of soft wood with a mass of 0.072 kg rests on a horizontal frictionless surface. A bullet with a mass of 4.67 g is fired with a

Question

A thin block of soft wood with a mass of 0.072 kg rests on a horizontal frictionless surface. A bullet with a mass of 4.67 g is fired with a speed of 619 m/s at a block of wood and passes completely through it. The speed of the block is 22 m/s immediately after the bullet exits the block.

Required:
Determine the speed of the bullet as it exits the block.

in progress 0
Nem 4 years 2021-07-20T19:31:13+00:00 1 Answers 16 views 0

Answers ( )

  1. minhkhoi
    0
    2021-07-20T19:32:20+00:00
    Reply

    Answer:

    v’= 279.66 m / s

    Explanation:

    We work this exercise using the conservation of the moment. For this we define the system formed by the two blocks, therefore the forces during the collision are internal of the action and reaction type.

    Initial instant. Before the crash

            p₀ = m v₀ + 0

    Final moment. After the crash

            p_f = m v + M v ’

    how the tidal wave is preserved

           p₀ = p_f

           m v₀ = m v + M v ’

           v =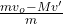 \frac{m v_o - Mv'}{m}

    let’s calculate

           v ’=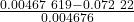 \frac{0.00467 \ 619 - 0.072 \ 22}{0.004676}

           v ’= \frac{2.89- 1.584}{ 0.00467}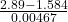

           v ’= 279.66 m / s

Leave an answer

Browse

Giải phương trình 1 ẩn: x + 2 - 2(x + 1) = -x . Hỏi x = ? ( )