Share
a student takes two subjects A and B. Know that the probability of passing subjects A and B is 0.8 and 0.7 respectively. If you have passed
Question
a student takes two subjects A and B. Know that the probability of passing subjects A and B is 0.8 and 0.7 respectively. If you have passed subject A, the probability of passing subject B is 0.8. Find the probability that the student passes both subjects? Find the probability that the student passes at least one of the two subjects
in progress
0
Mathematics
4 years
2021-08-06T21:32:11+00:00
2021-08-06T21:32:11+00:00 1 Answers
28 views
0

Answers ( )
Answer:
0.64 = 64% probability that the student passes both subjects.
0.86 = 86% probability that the student passes at least one of the two subjects
Step-by-step explanation:
Conditional Probability
We use the conditional probability formula to solve this question. It is
In which
P(B|A) is the probability of event B happening, given that A happened.
P(A) is the probability of A happening.
In this question:
Event A: Passing subject A
Event B: Passing subject B
The probability of passing subject A is 0.8.
This means that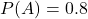
If you have passed subject A, the probability of passing subject B is 0.8.
This means that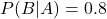
Find the probability that the student passes both subjects?
This is . So
. So
0.64 = 64% probability that the student passes both subjects.
Find the probability that the student passes at least one of the two subjects
This is:
Considering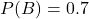 , we have that:
, we have that:
0.86 = 86% probability that the student passes at least one of the two subjects