Share
A sound measures 42 dB. The intensity of a second sound is four times as great. What is the decibel level of this second sound?
Question
A sound measures 42 dB. The intensity of a second sound is four times as great. What is the decibel level of this
second sound?
in progress
0
Mathematics
4 years
2021-08-15T11:28:44+00:00
2021-08-15T11:28:44+00:00 1 Answers
274 views
0

Answers ( )
Answer:
The decibel level of this second sound is 48.021 decibels.
Step-by-step explanation:
The acoustic intensity (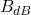 ), measured in decibels, is defined by the following formula:
), measured in decibels, is defined by the following formula:
Where:
If we know that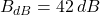 and
and 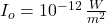 , then the real sound intensity of the first sound is:
, then the real sound intensity of the first sound is:
The real sound intensity of the second sound is four times greater, that is:
If we know that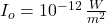 and
and 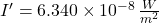 , then the acoustic intensity of the second sound is:
, then the acoustic intensity of the second sound is:
The decibel level of this second sound is 48.021 decibels.