A solid sphere of radius R is placed at a height of 30 cm on a15 degree slope. It is released and rolls, without slipping, to the bottom.

Question

A solid sphere of radius R is placed at a height of 30 cm on a15 degree slope. It is released and rolls, without slipping, to the bottom.

a) From what height should a circular hoop of radius R bereleased on the same slope in order to equal the sphere’s speed atthe bottom?
b) Can a circular hoop of different diameter be released froma height of 30 cm and match the sphere’s speed at the bottom? If,so what is the diameter? If not, why not?

in progress 0
Hưng Khoa 3 years 2021-07-16T20:15:17+00:00 1 Answers 437 views 0

Answers ( )

  1. phucdien
    0
    2021-07-16T20:17:08+00:00
    Reply

    Answer:

    The height is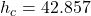  h_c = 42.857

    A circular hoop of different diameter cannot be released from a height 30cm and match the sphere speed because from the conservation relation the speed of the hoop is independent of the radius (Hence also the diameter )

    Explanation:

       From the question we are told that

               The height is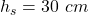 h_s = 30 \ cm

                The angle of the slope is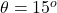 \theta = 15^o

    According to the law of conservation of energy

         The potential energy of the sphere at the top of the slope = Rotational kinetic energy + the linear kinetic energy

                              mgh = \frac{1}{2} I w^2 + \frac{1}{2}mv^2

    Where I is the moment of inertia which is mathematically represented as this for  a sphere

                        I = \frac{2}{5} mr^2

      The angular velocity w is mathematically represented as

                             w = \frac{v}{r}

    So the equation for conservation of energy becomes

                   mgh_s = \frac{1}{2} [\frac{2}{5} mr^2 ][\frac{v}{r} ]^2 + \frac{1}{2}mv^2

                  mgh_s = \frac{1}{2} mv^2 [\frac{2}{5} +1 ]

                 mgh_s = \frac{1}{2} mv^2 [\frac{7}{5} ]

                gh_s =[\frac{7}{10} ] v^2

                  v^2 = \frac{10gh_s}{7}

    Considering a circular hoop

       The moment of inertial is different for circle and it is mathematically represented as

                 I = mr^2

    Substituting this into the conservation equation above

                  mgh_c = \frac{1}{2} (mr^2)[\frac{v}{r} ] ^2 + \frac{1}{2} mv^2

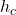    Where h_c is the height where the circular hoop would be released to equal the speed of the sphere at the bottom

                     mgh_c = mv^2

                         gh_c = v^2

                         h_c = \frac{v^2}{g}

    Recall that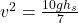   v^2 = \frac{10gh_s}{7}

                        h_c= \frac{\frac{10gh_s}{7} }{g}

                          = \frac{10h_s}{7}

                Substituting values

                       h_c = \frac{10(30)}{7}

                           h_c = 42.86 \ cm    

           

         

                             

Leave an answer

Browse

Giải phương trình 1 ẩn: x + 2 - 2(x + 1) = -x . Hỏi x = ? ( )