Share
A rod has a radius of 10 mm is subjected to an axial load of 15 N such that the axial strain in the rod is ????௫ = 2.75*10-6, determine the
Question
A rod has a radius of 10 mm is subjected to an axial load of 15 N such that the axial strain in the rod is ????௫ = 2.75*10-6, determine the modulus of elasticity E and the change in the rod’s diameter. Let Poisson’s ratio ν = 0.23.
in progress
0
Physics
3 years
2021-08-27T16:28:31+00:00
2021-08-27T16:28:31+00:00 1 Answers
40 views
0

Answers ( )
Answer:
Knowing we only have one load applied in just one direction we have to use the Hooke’s law for one dimension
ex = бx/E
бx = Fx/A = Fx/π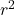
Using both equation and solving for the modulus of elasticity E
E = бx/ex = Fx / π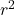 ex
ex
E =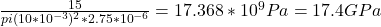
Apply the Hooke’s law for either y or z direction (circle will change in every direction) we can find the change in radius
ey =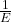 (бy – v (бx + бz)) =
(бy – v (бx + бz)) = 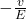 бx
бx
=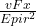 =
= 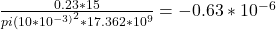
Finally
ey = Δr / r
Δr = ey * r = 10 *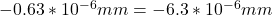
Δd = 2Δr =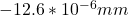
Explanation: