A radioactive isotope is decaying at a rate of 15% every hour. Currently there are 150 grams of the substance. Write an equation that will r

Question

A radioactive isotope is decaying at a rate of 15% every hour. Currently there are 150 grams of the substance. Write an equation that will represent the number of grams present after n hours. How much will be left one day from now?A radioactive isotope is decaying at a rate of 15% every hour. Currently there are 150 grams of the substance. Write an equation that will represent the number of grams present after n hours. How much will be left one day from now?

in progress 0
Hưng Khoa 3 years 2021-08-14T23:04:36+00:00 1 Answers 5 views 0

Answers ( )

  1. phucdien
    0
    2021-08-14T23:05:50+00:00
    Reply

    Answer:

    The equation that will represent the number of grams present after n hours is A(n) = 150(0.85)^n

    3.035 grams will be left one day from now.

    Step-by-step explanation:

    Exponential equation for the amount of a substance:

    The exponential equation for the amount of a substance is given by:

    A(t) = A(0)(1-r)^t

    In which A(0) is the initial amount and r is the decay rate, as a decimal, and t is the time period.

    A radioactive isotope is decaying at a rate of 15% every hour.

    This means that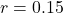 r = 0.15

    Currently there are 150 grams of the substance.

    This means that A(0) = 150

    Write an equation that will represent the number of grams present after n hours.

    A(n) = A(0)(1-r)^n

    A(n) = 150(1-0.15)^n

    A(n) = 150(0.85)^n

    How much will be left one day from now?

    One day is 24 hours, so this is A(24).

    A(24) = 150(0.85)^{24} = 3.035

    3.035 grams will be left one day from now.

Leave an answer

Browse

Giải phương trình 1 ẩn: x + 2 - 2(x + 1) = -x . Hỏi x = ? ( )