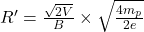A proton (mass mp), a deuteron (m = 2mp, Q = e), and an alpha particle (m = 4mp, Q = 2e), are accelerated by the same potential difference V

Question

A proton (mass mp), a deuteron (m = 2mp, Q = e), and an alpha particle (m = 4mp, Q = 2e), are accelerated by the same potential difference V and then enter a uniform magnetic field B where they move in circular paths perpendicular to B. Determine the radius of the paths for the deuteron and alpha particle in terms of that for the proton.

in progress 0
Thiên Thanh 4 years 2021-07-28T21:33:42+00:00 1 Answers 59 views 0

Answers ( )

  1. Dulcie
    0
    2021-07-28T21:35:24+00:00
    Reply

    Answer with Explanation:

    We are given that

    Mass of deuteron=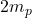2m_p

    Charge, Q=e

    Mass of alpha particle=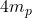4m_p

    Charge,q=2e

    Magnetic field=B

    Mass of proton=m_p

    Let radius of path of proton=r

    v=\sqrt{\frac{2qV}{m}}

    Using the formula

    Velocity of proton=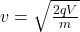v=\sqrt{\frac{2qV}{m}}

    Centripetal force =Magnetic force

    \frac{mv^2}{r}=qvB

    r=\frac{mv}{qB}

    Radius of proton,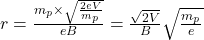r=\frac{m_p\times\sqrt{\frac{2eV}{m_p}}}{eB}=\frac{\sqrt{2V}}{B}\sqrt{\frac{m_p}{e}}

    Radius of deuteron,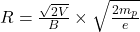R=\frac{\sqrt{2V}}{B}\times \sqrt{\frac{2m_p}{e}}

    \frac{R}{r}=\sqrt{2}

    R=\sqrt{2}r

    Radius of alpha particle,R'=\frac{\sqrt{2V}}{B}\times\sqrt{\frac{4m_p}{2e}}

    \frac{R'}{r}=\sqrt 2

    R'=\sqrt{2} r

Leave an answer

Browse

Giải phương trình 1 ẩn: x + 2 - 2(x + 1) = -x . Hỏi x = ? ( )