Share
A plastic dowel has a Young’s Modulus of 1.50 ✕ 1010 N/m2. Assume the dowel will break if more than 1.50 ✕ 108 N/m2 is exerted. (a) What is
Question
A plastic dowel has a Young’s Modulus of 1.50 ✕ 1010 N/m2. Assume the dowel will break if more than 1.50 ✕ 108 N/m2 is exerted. (a) What is the maximum force (in kN) that can be applied to the dowel assuming a diameter of 2.70 cm? kN (b) If a force of this magnitude is applied compressively, by how much (in mm) does the 28.0 cm long dowel shorten? (Enter the magnitude.) mm
in progress
0
Physics
4 years
2021-08-06T17:55:27+00:00
2021-08-06T17:55:27+00:00 1 Answers
34 views
0

Answers ( )
Answer:
(A) The maximum force is 85.8 kN.
(B) Dowel shorten by 2.79 mm
Explanation:
Given:
Young modulus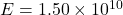

Pressure fracture

Diameter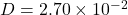 m
m
Radius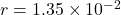 m
m
(A)
From the formula of force in terms of pressure,
Where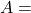 area of dowel
area of dowel
(B)
From young modulus formula,
Where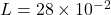 m
m
Therefore, the maximum force is 85.8 kN and dowel shorten by 2.79 mm