Share
A particle carrying charge +q is placed at the center of a thick-walled conducting shell that has inner radius R and outer radius 2R and car
Question
A particle carrying charge +q is placed at the center of a thick-walled conducting shell that has inner radius R and outer radius 2R and carries charge −2q. A thin-walled conducting shell of radius 5R carries charge +2q and is concentric with the thick-walled shell. Define V = 0 at infinity. Calculate all distances from the particle at which the electrostatic potential is zero.
in progress
0
Physics
3 years
2021-07-25T15:20:30+00:00
2021-07-25T15:20:30+00:00 1 Answers
19 views
0

Answers ( )
Answer:
10R/11 and 5R/2
Explanation:
The radius of the conducting shell = R,
Electrostatic potential inside the shell (r<R) = kq/R
Electrostatic potential outside the shell (r>R) = kq/r
If x is the point of zero potential
Electrostatic potential for inner shell,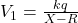
Electrostatic potential for outer shell,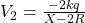
Electrostatic potential for the thin walled shell,
The values of X=r that satisfy the above equation are 10R/11 and 5R/2