A new DVD is available for sale in a store one week after its release. The cumulative revenue, $R, from sales of the DVD in this store in week t after its release is R=f(t)=350 ln tR=f(t)=350lnt with t>1.
Find f(5), f'(5), and the relative rate of change f’/f at t=5. Interpret your answers in terms of revenue.
Question
Solution :
It is given that :
[tex]$f'(t) = (350 \ln t)’$[/tex]
[tex]$=350(\ln t)’$[/tex]
[tex]$=\frac{350}{t}$[/tex]
So, [tex]f(5)=350 \ln (5) \approx 563[/tex]
[tex]$f'(5) = \frac{350}{5}$[/tex]
[tex]=70[/tex]
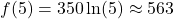
The relative change is then,
[tex]$\frac{f'(5)}{f(5)}=\frac{70}{350\ \ln(5)}$[/tex]
[tex]$=\frac{1}{5\ \ln(5)}$[/tex]
[tex]$\approx 0.12$[/tex]
[tex]=12\%[/tex]
This means that after 5 weeks, the revenue from the DVD sales in $563 with a rate of change of $70 per week and the increasing at a continuous rate of 12% per week.