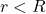Share
A long, straight wire of radius R carries a steady current I that is uniformly distributed through the cross section of the wire. Calculate
Question
A long, straight wire of radius R carries a steady current I that is uniformly distributed through the cross section of the wire. Calculate the magnetic field a distance r from the center of the wire in regions r ≥ R and r < R.
in progress
0
Physics
4 years
2021-08-04T08:41:09+00:00
2021-08-04T08:41:09+00:00 1 Answers
15 views
0

Answers ( )
Answer:
a
When
b
When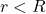
Explanation:
From the question we are told that
The radius is R
The current is I
The distance from the center
Ampere’s law is mathematically represented as
When
=>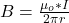
But when