A firework is designed so that when it is fired directly upwards, it explodes and splits into three equal-massed parts at its peak. Someone

Question

A firework is designed so that when it is fired directly upwards, it explodes and splits into three equal-massed parts at its peak. Someone launches the firework directly upwards and measures the locations of two of the pieces of the firework. They find that one piece landed 2 meters to the left and another piece landed two meters behind them. Where did the third piece land? Assume that none of the three parts went further upward after the explosion.

in progress 0
Amity 4 years 2021-07-18T01:05:08+00:00 1 Answers 76 views 0

Answers ( )

  1. minhkhang
    0
    2021-07-18T01:06:54+00:00
    Reply

    Answer:

    the third piece landed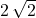 2\,\sqrt{2}  meters in a direction 45 degrees from the observer’s right towards the front

    Explanation:

    Due to conservation of momentum, the momentum of the third piece must add to the other two momenta in vector from to render zero  (initial momentum of the firework on a plane parallel to ground. Therefore the momentum components of the third piece must have a component to the right equal in magnitude to the momentum of the piece that traveled to the left, and a momentum component pointing to the front of the observer of equal magnitude to that of the piece that traveled behind the observer. Then the direction of the third momentum must be at 45 degrees from the observer’s right towards the observer’s front.

    Also, the magnitude of a momentum vector of such components, is given by the Pythagorean theorem. Recall also that the magnitudes of the momentum vectors of the first two pieces must be equal since they traveled equal distances.

    |P_3|=\sqrt{P_1^2+P_2^2} \\|P_3|=\sqrt{P^2+P^2}\\|P_3|=\sqrt{2P^2}\\|P_3|=P\sqrt{2}

    Then the distance traveled by the third piece must also keep this proportionality:

    D_3=\sqrt{2} \,\,D\\D_3=\sqrt{2} \,*\,2\,\,meters\\D_3=2\,\sqrt{2} \,\,meters

Leave an answer

Browse

Giải phương trình 1 ẩn: x + 2 - 2(x + 1) = -x . Hỏi x = ? ( )