A dielectric cube of side a, centered at the origin, carries a “frozen-in” polarization P = kr, where k is a constant. Find all the bound ch

Question

A dielectric cube of side a, centered at the origin, carries a “frozen-in” polarization P = kr, where k is a constant. Find all the bound charges and check that they add up to zero.

in progress 0
Trung Dũng 4 years 2021-07-31T18:21:40+00:00 1 Answers 972 views 0

Answers ( )

  1. thnahdat
    1
    2021-07-31T18:23:02+00:00
    Reply

    The total volume of bound charge is zero.

    Explanation:

    We have to the volume and surface bounded charge densities.

       ρb = – Δ . p = – Δ .k (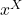x^{X} +y^{Y} +x^{Y})

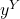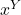                          = – 3k

     On the top of the cube the surface charge density is

                         σb = p . z

                               = \frac{ka}{2}

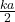
    By symmetry this holds for all the other sides. The total bounded charge should be zero

            Qtot = (-3k)a³ + 6 .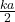 \frac{ka}{2} . a² = 0

                   σb = -3K σb =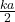 \frac{ka}{2}

                Qtot = 0

    Hence,  the total volume of bound charge is zero.

Leave an answer

Browse

Giải phương trình 1 ẩn: x + 2 - 2(x + 1) = -x . Hỏi x = ? ( )