A beam of light in air enters a glass slab with an index of refraction of 1.40 at an angle of incidence of 30.0°. What is the angle of refra

Question

A beam of light in air enters a glass slab with an index of refraction of 1.40 at an angle of incidence of 30.0°. What is the angle of refraction? (index of refraction of air=1)

in progress 0
Euphemia 4 years 2021-08-05T09:09:31+00:00 1 Answers 85 views 0

Answers ( )

  1. Nick
    0
    2021-08-05T09:11:02+00:00
    Reply

    Answer:

    \boxed{\sf Angle \: of \: refraction \: (r) = {sin}^{ - 1} ( \frac{1}{2.8} )}

    Given:

    Refractive index of air (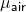 \sf \mu_{air} )= 1

    Refractive index of glass slab (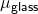 \sf \mu_{glass} ) = 1.40

    Angle of incidence (i) = 30.0°

    To Find:

    Angle of refraction (r)

    Explanation:

    From Snell’s Law:

    \boxed{ \bold{ \sf \mu_{air}sin \ i = \mu_{glass}sin \: r}}

    \sf \implies 1 \times sin \: 30 ^ \circ = 1.4sin \:r

    \sf sin \:30^ \circ = \frac{1}{2} :

    \sf \implies \frac{1}{2} = 1.4 sin \: r

    \sf \frac{1}{2} = 1.4 sin \: r \: is \: equivalent \: to \: 1.4 sin \: r = \frac{1}{2} :

    \sf \implies 1.4 sin \: r = \frac{1}{2}

    Dividing both sides by 1.4:

    \sf \implies \frac{\cancel{1.4} sin \: r}{\cancel{1.4}} = \frac{1}{2 \times 1.4}

    \sf \implies sin \: r = \frac{1}{2 \times 1.4}

    \sf \implies sin \: r = \frac{1}{2.8}

    \sf \implies r = {sin}^{ - 1} ( \frac{1}{2.8} )

    \therefore

    \sf Angle \: of \: refraction \: (r) = {sin}^{ - 1} ( \frac{1}{2.8} )

Leave an answer

Browse

Giải phương trình 1 ẩn: x + 2 - 2(x + 1) = -x . Hỏi x = ? ( )