A beaker contains 0.500 kg of water at a temperature of 3.0 °C. The beaker is heated, and the internal energy of the water incr

Question

A beaker contains 0.500 kg of water at a temperature of 3.0 °C. The beaker is heated, and the
internal energy of the water increases by 21.0 kJ.
The specific heat capacity of water is 4200 J / (kg °C).
What is the temperature of the water after it has been heated?

in progress 0
Diễm Thu 3 years 2021-07-25T20:16:54+00:00 2 Answers 488 views 1

Answers ( )

  1. Giakhanh
    1
    2021-07-25T20:18:16+00:00
    Reply

    Answer:

    13°C

    Explanation:

    We can apply the formula for Heat energy gained by a body. It is given as:

    H = mc(T_2 - T_1)

    where m = mass of the body

    c = Specific heat capacity of the body

    T_2 = final temperature of the body

    T_1 = initial temperature of the body

    For the water in the beaker, we are given that:

    m = 0.5 kg

    T_1  = 3.0 °C

    H = 21 kJ = 21000 J

    c = 4200 J/kg°C

    Hence, the final temperature T_2 of the water is:

    21000 = 0.5 * 4200 * (T_2 – 3)

    21000 = 2100 * (T_2  – 3)

    (T_2  – 3) = \frac{21000}{2100}

    T_2  – 3 = 10

    T_2  = 10 + 3 = 13°C

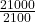
    The final temperature of the water is 13°C.

  2. niczorrrr
    1
    2021-07-25T20:18:50+00:00
    Reply

    Answer:

    The temperature of the water after it has been heated is 13°C

    Explanation:

    Heat capacity H is expressed as shown :

    H = mc∆t

    H is the internal energy of the water

    m is the mass of the water

    c is the specific heat capacity of the water

    ∆t is the change temperature

    Given H = 21kJ = 21,000Joules

    m = 0.500kg

    c = 4200 J / (kg °C).

    ∆t = t2-t1

    t2 is the final temperature

    t1 is the initial temperature = 3°C

    Substituting the parameters;

    21000 = 0.5(4200)(t2- 3)

    21000 = 2100(t2-3)

    21000 = 2100t2 – 6300

    2100t2 = 21000+6300

    2100t2 = 27300

    t2= 27300/2100

    t2 = 13°C

Leave an answer

Browse

Giải phương trình 1 ẩn: x + 2 - 2(x + 1) = -x . Hỏi x = ? ( )