Share
A 4.4 m diameter merry-go-round is rotating freely with an angular velocity of 0.80 rad/s. Its total moment of inertia is 1950 kg · m2. Four
Question
A 4.4 m diameter merry-go-round is rotating freely with an angular velocity of 0.80 rad/s. Its total moment of inertia is 1950 kg · m2. Four people standing on the ground, each of 50 kg mass, suddenly step onto the edge of the merry-go-round.
What is the angular velocity of the merry-go-round now?
in progress
0
Physics
4 years
2021-08-15T01:01:47+00:00
2021-08-15T01:01:47+00:00 1 Answers
8 views
0

Answers ( )
Answer:
Angular velocity of merry go round is 0.64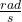 .
.
Explanation:
Given :
Radius of merry go round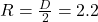 m
m
Angular velocity of merry go round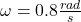
Momentum of inertia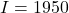
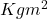
Mass of each people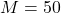 Kg
Kg
From the formula of angular momentum conservation,
So initial angular momentum,
Now we calculate the MOI after people jump on merry go round,
But there are four people so we have to multiply with 4 and add merry go round MOI,
So total MOI after people jump on is,
From conservation of angular momentum,
So angular velocity is,