Share
A 3.10 mol sample of an ideal diatomic gas expands adiabatically from a volume of 0.1550 m3 to 0.742 m3 . Initially the pressure was 1.00 at
Question
A 3.10 mol sample of an ideal diatomic gas expands adiabatically from a volume of 0.1550 m3 to 0.742 m3 . Initially the pressure was 1.00 atm.(a) Determine the initial and final temperatures.initial Kfinal K(b) Determine the change in internal energy. J(c) Determine the heat lost by the gas. J(d) Determine the work done on the gas. J
in progress
0
Physics
4 years
2021-07-15T12:28:45+00:00
2021-07-15T12:28:45+00:00 1 Answers
10 views
0

Answers ( )
Answer:
a) Initial Temperature = 609.4 K and Final Temperature = 325.7 K
b) the change in internal energy is -18279.78 J
c) heat lost by the gas is zero or 0
d) the work done on the gas is -18279.78 J
Explanation:
Given the data in the question;
P = 1 atm = 101325 pascal
= 1 atm = 101325 pascal
P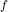 = ?
= ?
V = 0.1550 m³
= 0.1550 m³
V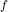 = 0.742 m³
= 0.742 m³
we know that for an adiabatic process γ = 1.4
P V
V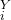 = P
= P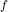 V
V
P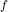 = P
= P [tex]([/tex] V
[tex]([/tex] V / V
/ V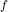
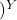
we substitute
P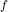 = 1 ×
= 1 ×  0.1550 / 0.742
0.1550 / 0.742 
= 0.2088948787
0.2088948787 
= 0.11166 atm
a) the initial and final temperatures
Initial temperature
T = P
= P V
V / nR
/ nR
given that n = 3.10 mol
= ( 101325 × 0.1550 ) / ( 3.10 × 8.314 )
= 15705.375 / 25.7734
T = 609.4 K
= 609.4 K
Final temperature
T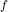 = P
= P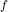 V
V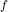 / nR
/ nR
= ( 0.11166 × 101325 × 0.742 ) / ( 3.10 × 8.314 )
= 8394.95 / 25.7734
= 325.7 K
Therefore, Initial Temperature = 609.4 K and Final Temperature = 325.7 K
b) the change in internal energy
ΔE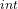 = nC
= nC ΔT
ΔT
here, C = ( 5/2 )R
= ( 5/2 )R
ΔE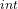 = 3.10 × ( 5/2 )8.314 × ( 325.7 – 609.4 )
= 3.10 × ( 5/2 )8.314 × ( 325.7 – 609.4 )
= -18279.78 J
Therefore, the change in internal energy is -18279.78 J
c) the heat lost by the gas
Since its an adiabatic process,
Q = 0
Therefore, heat lost by the gas is zero or 0
d) the work done on the gas
W = ΔE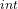 – Q
– Q
= -18279.78 J – 0
W = -18279.78 J
Therefore, the work done on the gas is -18279.78 J