A 170-km-long high-voltage transmission line 2.00 cm in diameter carries a steady current of 1,010 A. If the conductor is copper with a free

Question

A 170-km-long high-voltage transmission line 2.00 cm in diameter carries a steady current of 1,010 A. If the conductor is copper with a free charge density of 8.50 1028 electrons per cubic meter, how many years does it take one electron to travel the full length of the cable

in progress 0
Gerda 4 years 2021-08-17T15:38:32+00:00 1 Answers 9 views 0

Answers ( )

  1. Amity
    0
    2021-08-17T15:39:36+00:00
    Reply

    Answer:

    The number of years is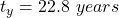 t_y = 22.8 \ years

    Explanation:

    From the question we are told that

        The length of the transmission line is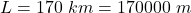  L = 170 \ km = 170000 \ m

        The diameter of the transmission line is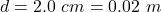  d = 2.0 \ cm = 0.02 \ m

         The current which the transmission line carry is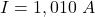  I = 1,010 \ A

          The charge density of the transmission line is  j = 8.50 *10^{28 } \ electron/m^3

    Now  the cross-sectional  area of the transmission line is mathematically represented  as

               A = \pi r^2

    Here r is the radius which is mathematically evaluated as

             r = \frac{d}{2}

    substituting values

             r = \frac{0.02}{2}

             r = 0.01 \ m

    Hence

           A = 3.142 * (0.01)^2

    =>      A = 3.142 *10^{-4} \ m^2

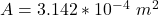
    Now the drift velocity of electron is mathematically evaluated as

            v = \frac{I}{j* e * A }

    Where e is the charge on one electron and the values is  e = 1.60 *10^{-19} \ C

           So

                  v = \frac{ 1010}{8.50 *10^{28}* (1.60 *10^{-19}) * 3.142*10^{-4} }

                  v = 2.363 *10^{-4} \ m/s

    Now the time taken is  mathematically evaluated as

                    t = \frac{L}{v }

    substituting values

                    t = \frac{170000}{2.363 *10^{-4} }

                    t = 7.194*10^{8}\ s

    Converting to years

           t_y = \frac{t}{365\ days * 24 \ hours * 3600\ seconds}

    substituting values

            t_y =\frac{7.194 *10^{8}}{365 *24 * 3600}

            t_y = 22.8 \ years

         

Leave an answer

Browse

Giải phương trình 1 ẩn: x + 2 - 2(x + 1) = -x . Hỏi x = ? ( )