A 133 kg horizontal platform is a uniform disk of radius 1.95 m and can rotate about the vertical axis through its center. A 62.7 kg person

Question

A 133 kg horizontal platform is a uniform disk of radius 1.95 m and can rotate about the vertical axis through its center. A 62.7 kg person stands on the platform at a distance of 1.19 m from the center, and a 28.5 kg dog sits on the platform near the person 1.45 m from the center. Find the moment of inertia of this system, consisting of the platform and its population, with respect to the axis.

in progress 0
Hưng Khoa 4 years 2021-08-17T14:47:17+00:00 1 Answers 20 views 0

Answers ( )

  1. thongdat2
    0
    2021-08-17T14:48:33+00:00
    Reply

    Answer:

    The moment of inertia of the system is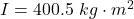  I = 400.5 \ kg \cdot m^2

    Explanation:

    From the question we are told that

        The mass of the platform is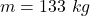  m = 133\ kg

         The  radius of the  platform is  r = 1.95 m

         The mass of the person is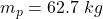 m_p = 62.7 \ kg

         The position of the person from the center is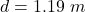  d = 1.19 \ m

           The mass of the dog is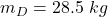 m_D = 28.5 \ kg

         The position of the dog from the center is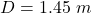  D = 1.45 \ m

       

    Generally the moment of inertia of the platform with respect to its axis is  mathematically represented as

           I_p = \frac{m r^2}{2}

    The  moment of inertia of the person with respect to the axis is mathematically represented as

            I_z = m_p* d^2

    The  moment of inertia of the dog with respect to the axis is mathematically represented as

           I_D = m_d * D^2

    So the moment of inertia of the system about the axis  is mathematically evaluated as

            I = I_p + I_z + I_D

    =>      I = \frac{mr^2}{2} + m_p * d^2 + m_d * D^2

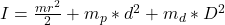
    substituting values  

                I = \frac{(133) * (1.95)^2}{2} + (62.7) * (1.19)^2 + (28.5) * (1.45)^2

              I = 400.5 \ kg \cdot m^2

Leave an answer

Browse

Giải phương trình 1 ẩn: x + 2 - 2(x + 1) = -x . Hỏi x = ? ( )