Consider the line y = 7x-3. What is the slope of a line parallel to this line? What is the slope of a line perpendicular to this

Question

Consider the line y = 7x-3.
What is the slope of a line parallel to this line?
What is the slope of a line perpendicular to this line?

in progress 0
Thanh Thu 4 years 2021-08-25T08:44:43+00:00 1 Answers 25 views 0

Answers ( )

  1. lethu
    0
    2021-08-25T08:45:50+00:00
    Reply

    Answer:

    Gradient of parallel line= 7

    Gradient of perpendicular line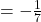 = - \frac{1}{7}

    Step-by-step explanation:

    The equation of the line is already in slope-intercept form (y= mx +c). This means that the coefficient of x is the gradient and the constant -3 is the y-intercept of the line.

    y= 7x -3

    Gradient= 7

    Parallel lines have the same gradient.

    Thus, the slope of the line parallel to this line is also 7.

    The product of the gradients of 2 perpendicular lines is -1.

    (Gradient of perpendicular line)(7)= -1

    Gradient of perpendicular line

    = -1 ÷7

    = - \frac{1}{7}

Leave an answer

Browse

Giải phương trình 1 ẩn: x + 2 - 2(x + 1) = -x . Hỏi x = ? ( )