An elementary school class ran one mile with a mean of 12 minutes and a standard deviation of three minutes. Rachel, a student in the class,

Question

An elementary school class ran one mile with a mean of 12 minutes and a standard deviation of three minutes. Rachel, a student in the class, ran one mile in seven minutes. A junior high school class ran one mile with a mean of nine minutes and a standard deviation of two minutes. Kenji, a student in the class, ran 1 mile in 8.5 minutes. A high school class ran one mile with a mean of seven minutes and a standard deviation of four minutes. Nedda, a student in the class, ran one mile in eight minutes.

Required:
a. Why is Kenji considered a better runner than Nedda, even though Nedda ran faster than he?
b. Who is the fastest runner with respect to his or her class? Explain why.

in progress 0
Thu Giang 3 years 2021-08-18T00:14:30+00:00 1 Answers 332 views 0

Answers ( )

  1. thanhha
    0
    2021-08-18T00:16:15+00:00
    Reply

    Answer:

    a) Since Kenji’s time has a lower Z-score’s than Nedda, he is considered a better runner relative to his competition.

    b) Since her time has the lowest Z-score, Rachel is the fastest runner with respect to her class.

    Step-by-step explanation:

    Z-score:

    In a set with mean \mu and standard deviation \sigma, the zscore of a measure X is given by:

    Z = \frac{X - \mu}{\sigma}

    The Z-score measures how many standard deviations the measure is from the mean. After finding the Z-score, we look at the z-score table and find the p-value associated with this z-score. This p-value is the probability that the value of the measure is smaller than X, that is, the percentile of X. Subtracting 1 by the pvalue, we get the probability that the value of the measure is greater than X.

    a. Why is Kenji considered a better runner than Nedda, even though Nedda ran faster than he?

    We have to see their z-scores.

    Whoever has the lower z-score is in the lower percentile of times, that is, runs faster.

    Kenji:

    A junior high school class ran one mile with a mean of nine minutes and a standard deviation of two minutes. Kenji, a student in the class, ran 1 mile in 8.5 minutes.

    So Kenji’s z-score is found when X = 8.5, \mu = 9, \sigma = 2. So

    Z = \frac{X - \mu}{\sigma}

    Z = \frac{8.5 - 9}{2}

    Z = -0.25

    Nedda:

    A high school class ran one mile with a mean of seven minutes and a standard deviation of four minutes. Nedda, a student in the class, ran one mile in eight minutes.

    So Nedda’s z-score is found when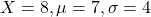 X = 8, \mu = 7, \sigma = 4. So

    Z = \frac{X - \mu}{\sigma}

    Z = \frac{8 - 7}{4}

    Z = 0.25

    Since Kenji’s time has a lower Z-score’s than Nedda, he is considered a better runner relative to his competition.

    b. Who is the fastest runner with respect to his or her class? Explain why.

    Whoever has the lower z-score.

    We have the z-scores for Kenji and Nedda, and we have to find Rachel’s z-score.

    An elementary school class ran one mile with a mean of 12 minutes and a standard deviation of three minutes. Rachel, a student in the class, ran one mile in seven minutes.

    So Rachel’s z-score is found when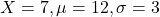 X = 7, \mu = 12, \sigma = 3

    Z = \frac{X - \mu}{\sigma}

    Z = \frac{7 - 12}{3}

    Z = -1.67

    Since her time has the lowest Z-score, Rachel is the fastest runner with respect to her class.

Leave an answer

Browse

Giải phương trình 1 ẩn: x + 2 - 2(x + 1) = -x . Hỏi x = ? ( )