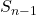Share
In an arithmetic sequence Sn=n^2SN=N^2-2N .USE formula (Tn=Sn-Sn-1) to determine the value of Tn
Question
In an arithmetic sequence Sn=n^2SN=N^2-2N .USE formula (Tn=Sn-Sn-1) to determine the value of Tn
in progress
0
Mathematics
4 years
2021-08-25T09:28:38+00:00
2021-08-25T09:28:38+00:00 1 Answers
24 views
0

Answers ( )
Answer:
Step-by-step explanation:
Given
Required
Find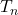
Calculate