Flying against the wind, an airplane travels 3800 kilometers in 4 hours. Flying with the wind, the same plane travels 3750 kilometers in 3 h

Question

Flying against the wind, an airplane travels 3800 kilometers in 4 hours. Flying with the wind, the same plane travels 3750 kilometers in 3 hours. What is the rate of the plane in still air and what is the rate of the wind?

in progress 0
Thu Nguyệt 4 years 2021-09-01T00:25:50+00:00 1 Answers 9 views 0

Answers ( )

  1. bonexptip
    0
    2021-09-01T00:27:06+00:00
    Reply

    Answer:

    V_w =1100 —- velocity of wind

    V_a = 150 — velocity of airplane

    Step-by-step explanation:

    Given

    V_a \to velocity of airplane

    V_w \to velocity of wind

    Flying with the wind, the distance (d) is:

    d = (V_w + V_a) * t

    Where d and t are distance travel and time spent with the wind

    So:

    3750 = (V_w + V_a) * 3

    Divide by 3

    1250 = (V_w + V_a)

    Flying against the wind, the distance (d) is:

    d = (V_w - V_a) * t

    Where d and t are distance travel and time against with the wind

    So:

    3800 = (V_w - V_a) * 4

    Divide by 4

    950 = (V_w - V_a)

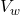    Make V_w the subject

    V_w= 950 + V_a

    Substitute: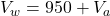 V_w= 950 + V_a in 1250 = (V_w + V_a)

    1250 = 950 + V_a + V_a

    1250 = 950 + 2V_a

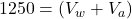
    Collect like terms

    2V_a = 1250 -950

    2V_a = 300

    Divide by 2

    V_a = 150

    Substitute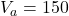 V_a = 150 in V_w= 950 + V_a

    V_w =950 +150

    V_w =1100

Leave an answer

Browse

Giải phương trình 1 ẩn: x + 2 - 2(x + 1) = -x . Hỏi x = ? ( )