What are the coordinates for the angle π/4 on tge unit circle

Question

What are the coordinates for the angle π/4 on tge unit circle

in progress 0
niczorrrr 4 years 2021-08-09T11:10:01+00:00 1 Answers 18 views 0

Answers ( )

  1. sori
    0
    2021-08-09T11:11:57+00:00
    Reply

    Answer: Both x and y are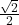 \frac{\sqrt{2}}{2} which is the same as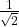 \frac{1}{\sqrt{2}}

    In other words, the point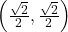 \left( \frac{\sqrt{2}}{2}, \frac{\sqrt{2}}{2} \right) is on the unit circle for the angle pi/4 radians. This point is equivalent to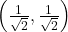 \left( \frac{1}{\sqrt{2}}, \frac{1}{\sqrt{2}}\right)

    ==============================================

    Explanation:

    The angle pi/4 radians is equivalent to 45 degrees. Draw out a 45-45-90 triangle with hypotenuse 1, and you’ll find the congruent legs are each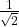 \frac{1}{\sqrt{2}} units long (apply the pythagorean theorem). If you apply the sine and cosine ratios, you’ll get the answer shown above.

    Recall that

    • x = cos(theta)
    • y = sin(theta)

    and also

    • cos = adjacent/hypotenuse
    • sin = opposite/hypotenuse

    The pythagorean theorem is a^2+b^2 = c^2.

Leave an answer

Browse

Giải phương trình 1 ẩn: x + 2 - 2(x + 1) = -x . Hỏi x = ? ( )