CNBC recently reported that the mean annual cost of auto insurance is 1013 dollars. Assume the standard deviation is 284 dollars. You take a

Question

CNBC recently reported that the mean annual cost of auto insurance is 1013 dollars. Assume the standard deviation is 284 dollars. You take a simple random sample of 56 auto insurance policies. Find the probability that a single randomly selected value is less than 995 dollars. P(X < 995)

in progress 0
Ben Gia 4 years 2021-07-29T05:46:45+00:00 1 Answers 25 views 0

Answers ( )

  1. Dau
    0
    2021-07-29T05:48:31+00:00
    Reply

    Answer:

    P(X < 995) = 0.4761

    Step-by-step explanation:

    Normal Probability Distribution

    Problems of normal distributions can be solved using the z-score formula.

    In a set with mean \mu and standard deviation \sigma, the z-score of a measure X is given by:

    Z = \frac{X - \mu}{\sigma}

    The Z-score measures how many standard deviations the measure is from the mean. After finding the Z-score, we look at the z-score table and find the p-value associated with this z-score. This p-value is the probability that the value of the measure is smaller than X, that is, the percentile of X. Subtracting 1 by the p-value, we get the probability that the value of the measure is greater than X.

    CNBC recently reported that the mean annual cost of auto insurance is 1013 dollars. Assume the standard deviation is 284 dollars.

    This means that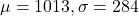 \mu = 1013, \sigma = 284

    Find the probability that a single randomly selected value is less than 995 dollars.

    This is the p-value of Z when X = 995. So

    Z = \frac{X - \mu}{\sigma}

    Z = \frac{995 - 1013}{284}

    Z = -0.06

    Z = -0.06 has a p-value of 0.4761. So

    P(X < 995) = 0.4761

Leave an answer

Browse

Giải phương trình 1 ẩn: x + 2 - 2(x + 1) = -x . Hỏi x = ? ( )