A satellite is in a circular orbit very close to the surface of a spherical planet. The period of the orbit is 2.17 hours. What is density o

Question

A satellite is in a circular orbit very close to the surface of a spherical planet. The period of the orbit is 2.17 hours. What is density of the planet

in progress 0
Ben Gia 4 years 2021-09-04T20:02:22+00:00 1 Answers 29 views 0

Answers ( )

  1. huyenthanh
    0
    2021-09-04T20:03:26+00:00
    Reply

    Explanation:

    Lets consider

    Circumference of orbit = T

    as it is mentioned in the question that a satellite is in orbit that is very close to the surface of planet. so

    circumference of orbit = circumference of planet

    Time period = T

    radius of planet = R

    orbital velocity = V

    gravitational constant = G

    mass of planet = m

    Solution:

    Time period for a uniform circular motion of orbit is,

    T =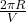 \frac{2\pi R}{V}

    T = \frac{2\pi R }{\sqrt{\frac{GM}{R} } }

    T= 2\pi \sqrt{(\frac{R^3}{GM} )}

    M = \frac{4}{3} \pi R^{3}p

    where p = density

    T = 2\pi \sqrt{\frac{R^{3} }{G\frac{4}{3}\pi R^{3} p } }

    T = \sqrt{\frac{3\pi }{Gp} }

    T = 2.17 hours = 7812 sec

    (7812)² = [( 3×3.14)/6.67×10^{-11}×ρ)]

    ρ = 6.28/6.67×10^{-11}×6.10×10^{-7}

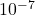
    ρ = 6.28/40.687×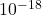10^{-18}

    ρ = 0.1543×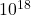10^{18}kg/m³

    ρ = 15.43×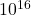10^{16}kg/m³

Leave an answer

Browse

Giải phương trình 1 ẩn: x + 2 - 2(x + 1) = -x . Hỏi x = ? ( )