Share
a 5.0 kg ball is dropped from a 2.5 m high window. what is the velocity of the ball just before it hits the ground?
Question
Lost your password? Please enter your email address. You will receive a link and will create a new password via email.
Answers ( )
Answer:
Approximately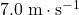 .
.
Assumption: the ball dropped with no initial velocity, and that the air resistance on this ball is negligible.
Explanation:
Assume the air resistance on the ball is negligible. Because of gravity, the ball should accelerate downwards at a constant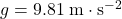 near the surface of the earth.
near the surface of the earth.
For an object that is accelerating constantly,
where
In this case, is the same as the change in the ball’s height:
is the same as the change in the ball’s height:  . By assumption, this ball was dropped with no initial velocity. As a result,
. By assumption, this ball was dropped with no initial velocity. As a result,  . Since the ball is accelerating due to gravity,
. Since the ball is accelerating due to gravity, 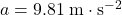 .
.
In this case, would be the velocity of the ball just before it hits the ground. Solve for
would be the velocity of the ball just before it hits the ground. Solve for