Share
square root A 1400 kg car is coasting on a horizontal road with a speed of 18 m/s . After passing over an unpaved, sandy stretch 35.0 m long
Question
square root A 1400 kg car is coasting on a horizontal road with a speed of 18 m/s . After passing over an unpaved, sandy stretch 35.0 m long, car’s speed has decreased to 14 m/s calculate net force
in progress
0
Physics
4 years
2021-08-27T19:06:30+00:00
2021-08-27T19:06:30+00:00 1 Answers
106 views
0

Answers ( )
Answer:
The net force on the car is 2560 N.
Explanation:
According to work energy theorem, the amount of work done is equal to the change of kinetic energy by an object. If ‘ ‘ be the work done on an object to change its kinetic energy from an initial value ‘
‘ be the work done on an object to change its kinetic energy from an initial value ‘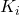 ‘ to the final value ‘
‘ to the final value ‘ ‘, then mathematically,
‘, then mathematically,
where ‘ ‘ is the mass of the object and ‘
‘ is the mass of the object and ‘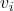 ‘ and ‘
‘ and ‘ ‘ be the initial and final velocity of the object respectively. If ‘
‘ be the initial and final velocity of the object respectively. If ‘ ‘ be the net force applied on the car, as per given problem, and ‘
‘ be the net force applied on the car, as per given problem, and ‘ ‘ is the displacement occurs then we can write,
‘ is the displacement occurs then we can write,
Given,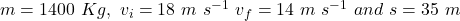 .
.
Equating equations (I) and (II),