Share
A runner of mass 54.0 kg runs around the edge of a horizontal turntable mounted on a vertical, frictionless axis through its center. The run
Question
A runner of mass 54.0 kg runs around the edge of a horizontal turntable mounted on a vertical, frictionless axis through its center. The runner’s velocity relative to the earth has magnitude 3.10 m/s. The turntable is rotating in the opposite direction with an angular velocity of magnitude 0.150 rad/s relative to the earth. The radius of the turntable is 2.80 m, and its moment of inertia about the axis of rotation is 85.0 kg*m2.Find the final angular velocity of the system if the runner comes to rest relative to the turntable. (You can treat the runner as a particle.)answer in rad/s please
in progress
0
Physics
4 years
2021-08-21T03:49:25+00:00
2021-08-21T03:49:25+00:00 1 Answers
153 views
0

Answers ( )
Explanation:
Angular speed of the turntable is = -0.150 rad/s.
Radius of the turntable is R = 2.80 m
Moment of inertia of the turntable is I = 85
Mass of the runner is M = 54 kg
Magnitude of the runner’s velocity relative to the earth is = 3.10 m/s.
Now, according to the law of conservation of angular momentum
And, the final angular speed of the system is
=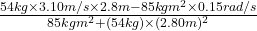
=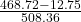
= 0.896 rad/s
Thus, we can conclude that the final angular velocity of the system if the runner comes to rest relative to the turntable is 0.896 rad/s.
= 0.611 rad/s